8  Higher Levels of Abstraction

Alec Loudenback

“Simple things should be simple, complex things should be possible.” — Alan Kay (1970s)

8.1 Chapter Overview

Why we talk about abstraction as a technique in and of itself, discussion of abstraction at the level of code organization and interfaces.

8.2 Introduction

In programming and modeling, as in mathematics, abstraction permits the definition of interchangeable components and patterns that can be reused. Abstraction is a selective ignorance—focusing on the aspects of the problem that are relevant, and ignoring the others. The last two chapters described what we might call “micro” level abstractions: specific functions or types.

In this chapter, we zoom out and examine some principles that guide good model development, manifesting in architectural concerns such as how different parts of the code are organized, what parts of the program are considered ‘public’ versus ‘private’, and patterns themselves.

Chapter 5 Described a number of tools that we can utilize as interfaces within our model. We use these tools that are provided by our programming language in service of the conceptual abstraction described above.

  • Functions let us implement behavior, where we need trouble ourselves with the low level details.
  • Data types provide a hierarchical structure to provide meaning to things, and to group those things together into more meaningful structures.
  • Modules allow us to combine data, and or function, into a related group of concepts which can be shared in different parts of our model

8.3 Principles for Abstraction

Here is a list of some principles that arise when developing a particular abstraction. Not all abstractions serve all of these purposes but generally fit one or more of them.

Table 8.1: Finding abstractions generally means finding patterns that fit into one of these principles.
Principle What Why Example
Separation of Concerns Divide the system into distinct parts, each addressing a separate concern Promote modularity and reduce high degree of dependence (coupling) between components Separating data retrieval, data processing, and output generation steps in a process
Encapsulation Hide the internal details of a component and expose only a clean, well-defined set of functionality (interface) Don’t let other parts of the program modify internal data and make the system easier to understand and maintain Defining a type or module with well defined behavior and responsibility
Composability Design simple components that can be combined to create more complex behaviors, as opposed to a single component that attempts to handle all behavior. Promote reuse and allow for the components to be combined creatively Separate details about economic conditions into different types than contracts/instruments
Generalization Identify common patterns and create generic components that can be specialized as needed. Often this means identifying the common behavior that arises repeatedly in a model Avoid duplication and make the system more expressive and extensible Defining a generic Instrument type that can be specialized for different asset classes

These principles provide guidance for creating abstractions that are modular, reusable, and maintainable. By following these principles, developers can create financial models that are easier to understand, extend, and adapt to changing requirements.

8.3.1 Pragmatic Considerations for Model Design

8.3.1.1 Behavior-Oriented

This strategies is to effectively group together components with a model that behaves similarly. So, in our example of bonds and interest-rate swaps fundamentally, they share many characteristics and are used in very similar ways within a model. Therefore, it might make sense to group them together when developing a model.

8.3.1.2 Domain Expertise

It may be that components of the model require sufficient expertise that different persons or groups are involved in the development. This may warrant separating a models design, So that different groups contributing to the model can focus on any more narrow aspect, Regardless of inherent similarity of components. For example, at a higher vertical level of obstruction, financial derivatives may fall under similar grouping, but sufficient differences exist for equity credit or foreign exchange derivatives that the model should separate those three asset classes for development purposes.

8.3.1.3 Composability versus All-in-One

For some model design goals, it may be warranted to attempt to bundle together more functionality instead of allowing users to compose a functionality that comes from different packages. For example, perhaps a certain visualization of a model result is particularly useful, It is not easy to create from scratch, And virtually everyone using the model, will desire to see the model output visualized that way. Instead of relying on the user to install a separate visualization package and develop the visualization themselves, it could make sense to bundle visualization functionality with a model that is otherwise unconcerned with graphical capabilities.

In general, though it is preferred to try to loosely couple systems, you can pick and choose which components you use and that those components work well together.

8.4 Interfaces

Interfaces are the boundary between different encapsulated abstractions. The user-facing interface is the set of functionality and details that the user of the package or model must consider, which is separate from the intermediate variables, logic, and complexity that may be contained within.

NoteExample of an interface

When looking up a ticker for a market quote, one need not be mindful of the underlying realtime databases, networking, rendering text to the screen, memory management, etc. The interface is “put in symbol, get out number”. By design, there are multiple layers of interfaces and abstractions used under the hood, but the financial modeler need only be actively concerned about the points that he or she comes in contact with, not the entire chain of complexity.

For a financial model this might mean that there is an interface for bonds, or there is an interface for interest-rate swaps. There may be a different interface for calculating risk metrics or visualizing the results.

Financial model this might mean that there is an interface for bonds, or there is an interface for interest-rate swaps. There may be a different interface for calculating risk metrics or visualizing the results. A better system design will separate the concern of visualizing output from the mechanics of a fixed income contract. This is what it means to put boundaries on different parts of a models logic. One of the easiest places to see this is with the available open source packages. There are packages available for visualizations, data frames, file, storage, statistical analysis, etc. for many of these it’s easy to see where the natural boundary lies.

However, it’s often difficult to find where to draw lines within financial models. For example, should bonds and interest-rate swaps be in separate packages? Or both part of a broader fixed income package? This is where much of the art and domain expertise of the financial professional comes to bear in modeling. There would be no way for a pure software engineer to think about the right design for the system without understanding how underlying components share, similarities or differences and how those components interact.

8.4.1 Defining Good Interfaces

A well-designed interface should follow these principles:

  1. Be minimal and focused. The interface should provide only the essential functionality needed, without unnecessary clutter or features. This makes the interface easier to understand and and facilitates building the necessary complexity through digestible, composable components.
  2. Be consistent and intuitive. The interface should use consistent naming conventions, parameter orders, and behaviors. It should match the user’s mental model and expectations.
  3. Hide implementation details. The interface should abstract away the internal complexity and expose only what the user needs to know. This of details allows the implementation to change without affecting users of the interface.
  4. Be documented and contractual. The interface should clearly specify what inputs it expects and what outputs or behaviors it provides. It forms a contract between the implementation and the users.
  5. Be testable. A good interface allows the functionality to be easily tested through the public interface, without needing to access internal details.

8.4.2 Interfaces: A Financial Modeling Case Study

As a case study, we’ll look at the FinanceModels.jl and related packages to discuss some of the background and design choices that went into the functionality. This suite was written by one of the authors and is publically available as set of installable Julia packages.

8.4.2.1 Background

In actuarial work, it is common to need to work with interest rate and bond yield curves to determine current forward rates, estimates of the shape of future yield curves, or discount a series of cashflows to determine a present value. Determining things like “given a par yield curve, what’s the implied discount factor for a cashflow at time 10” or “what is the 10 year BBB public corporate rate implied by the current curve in five years’ time” is cumbersome at best in a spreadsheet.

For example, to determine the answer to the first one (“a discount factor for time 10”) actually requires quite a bit of detail and assumption to derive:

  • Reference market data and a specification for how that market data should be interpreted. For example, if given the rate 0.05 for time 10, quoted as a continuous rate or annual effective? Is that a par rate, a zero-coupon bond (spot) rate, or a one-year-forward rate from time 10?
  • Smoothing, interpolation, or extrapolation for noisy or sparse data. Should the rates be bootstrapped or fit to a parametrically specified curve?

This is the type of complexity that we wish to save the user from needing to keep front of mind when the primary goal is, e.g., valuation of a stream of riskless life insurance payments, which might look like this:

risk_free_rates = [0.05,0.06,...0.06]
tenors = [1/12,3/12,...30]
yield_curve = Yields.Par(risk_free_rates,tenors)

cashflow_vector = [1e6,3e6,...,1e3]
present_value(yield_curve,cashflow_vector)

This is very clear from the variable and function names what the purpose and steps in the analysis are. Imagine starting with rates and cashflows in a spreadsheet, needing to perform the bootstrapping, interpolation, and discounting before getting to the simple present value sought in the analysis. What can be, with the right abstractions, distilled into five lines of code would take hundreds of cells in a spreadsheet. Providing abstractions like this at the hand of financial modelers is a productivity multiplier.

8.4.2.2 Initial Versions

There were two main abstractions to talk about from early versions of the packages.

8.4.2.2.1 Rates

Utilizing the benefit of the type system, it was decided that it would be most useful to represent rates not as simple floating point numbers (e.g. 0.05) but instead with dedicated types to distinguish between rate conventions. The abstract type CompoundingFrequency had two subtypes: Continuous and Periodic sop that a 5% rate compounded continuously versus an effective per period rate would be distinguished via Continuous(0.05) versus Periodic(0.05,1). The two could be converted between by extending the built-in Base.convert function.

This was useful because once rates were converted into Rates within the ecosystem, that data contained within itself characteristics that could distinguish how downstream functionality should treat the rates.

8.4.2.2.2 Yield Curves

At first, only bootstrapping was supported as a method to construct curve objects. This required that there was only one rate given per time period (no noisy data) and only supported linear, quadratic, and cubic splines.

Further, there was a specific constructor for different common types of instruments. From the old documentation:

  • Yields.Zero(rates,maturities) using a vector of zero, or spot, rates
  • Yields.Forward(rates,maturities) using a vector of one-period
  • Yields.Constant(rate) takes a single constant rate for all times
  • Yields.Par(rates,maturities) takes a series of yields for securities priced at par.Assumes that maturities <= 1 year do not pay coupons and that after one year, pays coupons with frequency equal to the CompoundingFrequency of the corresponding rate.
  • Yields.CMT(rates,maturities) takes the most commonly presented rate data (e.g. Treasury.gov) and bootstraps the curve given the combination of bills and bonds.
  • Yields.OIS(rates,maturities) takes the most commonly presented rate data for overnight swaps and bootstraps the curve.

This covered a lot of lightweight use-cases, but made a lot of implicit assumptions about how the given rates should be interpreted.

8.4.2.3 The Birth of FinanceModels

There were a multiple of insights that led to a more flexible interface in more recent versions.

A conceptual sketch of FinanceModels.jl components.

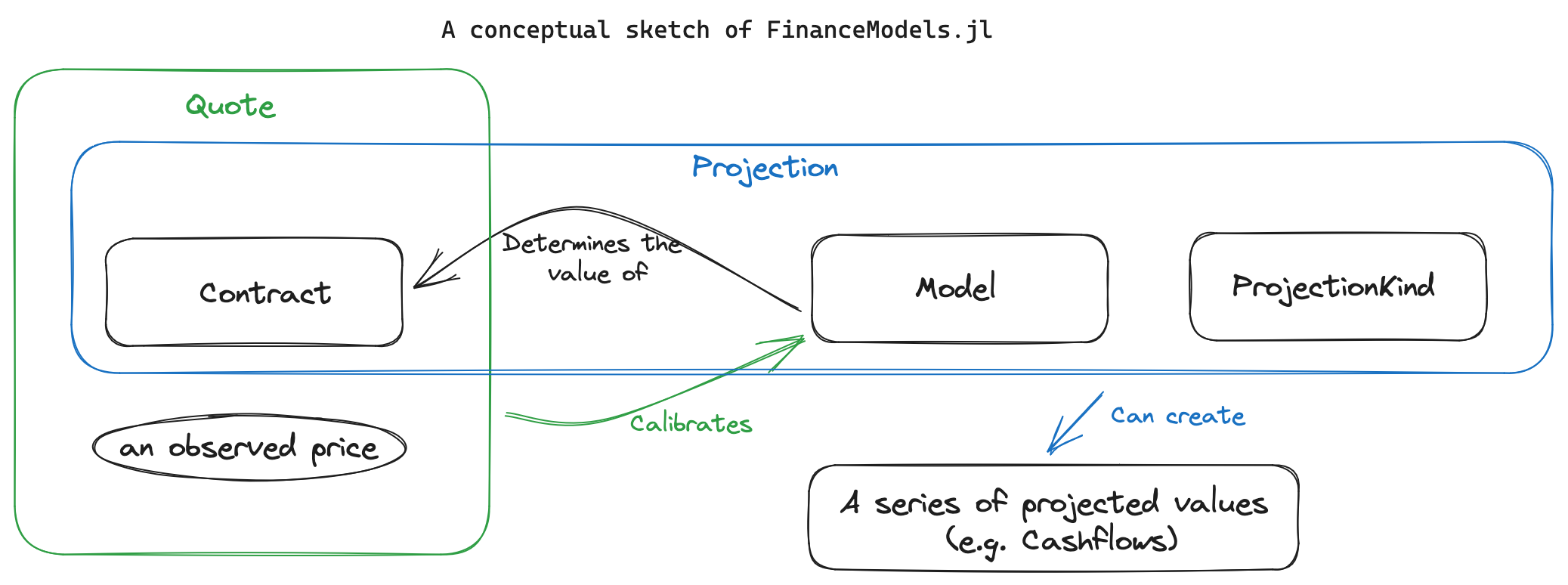
First, realizing that yield curves were just a particular kind of model - one that used interest rates to discount cashflows. But you can have different kinds of models - such as Black-Scholes option valuation or a Monte Carlo valuation approach. Likewise, the cashflows need not simply be a vector of floating point values, and instead it could be the representation of a generic financial contract. As long as the model knew how to value it, an appropriate present value could be derived.

Where previously it was:

present_value(yield_curve,cashflow_vector)

Now, it was

present_value(model,contract)

Second, that a model was simple some generic box that had been “fit” to previously observed prices for similar types of contracts we would be trying to value in the model. The combination of a contract and a price constituted a “quote” and with multiple quotes a model could be fit using various algorithms.

With these changes, the package that was originally called Yields.jl was renamed to FinanceModels.jl. The updated code from the earlier example now would e implemented like this:

risk_free_rates = [0.05,0.06,...0.06]
tenors = [1/12,3/12,...30]
quotes = ParYield.(risk_free_rates,tenors)
model = fit(Spline.Cubic(), quotes, Fit.Bootstrap())

cashflow_vector = [1e6,3e6,...,1e3]
present_value(model,cashflow_vector)

It’s slightly more verbose, but notice how much more powerful and extensible fit(Spline.Cubic(), quotes, Fit.Boostrap() is than Yields.Par(risk_free_rates,tenors) . The end result is the same, but now the same package and interface can clearly interchange other options, such as a NelsonSiegelSvennson curve instead of a spline. And the quotes could be a combination of observed bonds of different technical parameters (though still sharing characteristics which make it relevant for the model being constructed).

The same pattern also applies for option valuation, such as this example of vanilla euro options with an assumed constant volatility assumption:

1a = Option.EuroCall(CommonEquity(), 1.0, 1.0)
b = Option.EuroCall(CommonEquity(), 1.0, 2.0)

2qs = [
    Quote(0.0541, a),
    Quote(0.072636, b),
]

3model = Equity.BlackScholesMerton(0.01, 0.02, Volatility.Constant())

4m = fit(model, qs)

5present_value(m,qs[1].instrument)
1
The arguments to EuroCall are the underlying asset type, strike, and maturity time.
2
A vector of observed option prices.
3
A BSM model with a given risk free rate, dividend yield, and a to-be-fit constant volatility component.
4
Fits the model and derives an approximate volatility of 0.15 .
5
Values the contract and in such a simple, noiseless model we recover the original price of 0.0541

With a consistent interface able to handle a wide variety of situations, the modeler is free to expand the model in new directions of analysis with the built in functionality allowing him or her to compose pieces together that was not possible with the less abstracted design. For example, the equity option example had no parallel when all of the available constructors were Yields.Zero or Yields.Par and would have required a completely from-scratch implementation with newly defined functions.

Further, and critically, the new design allows modelers to create their own models or contracts1 and extend the existing methods rather than needing to create their own: the function signature fit(model,quotes) handles a very wide variety of cases, as does present_value(model,contract).

8.5 Macros & Homoiconicity

We’ve talked about transforming data and restructuring logic in order to make the model more effective. We can go still deeper!(Or is it higher level?) We can actually abstract the process of writing code itself! This subject is a bit advanced, so we are simply going to introduce it because you will likely find many convenient instances of it as a user even if you never find a need to implement this yourself.

Homoiconicity refers to the property of a programming language where the language’s code can be represented and manipulated as a data structure in the language itself. Think of a recipe. You can follow the recipe’s instructions (the code) to bake a cake. But you could also treat the recipe itself as data: you could write a program to scan thousands of recipes, find every instance of ‘sugar,’ and reduce the quantity by 25%. This is the essence of homoiconicity: the code (the recipe) can also be treated as data to be manipulated.

In a homoiconic language like Julia, the code is data and can be treated as such. This enables powerful metaprogramming (i.e. code that writes other code) capabilities, where code can be generated or transformed during the compilation process.

Macros are a metaprogramming feature that leverage homoiconicity in Julia. They allow the programmer to write code that generates or manipulates other code at compile-time. Macros take code as input, transform it based on certain rules or patterns, and return the modified code which then gets compiled.

For example, a built-in macro is @time which will measure the elapsed runtime for a piece of code2.

@time exp(rand())

Will effectively expand to:

t0 = time_ns()
value = exp(rand())
t1 = time_ns()
println("elapsed time: ", (t1-t0)/1e9, " seconds")
value

Here it is when we run it:

@time exp(rand())
  0.000006 seconds
1.5193053860794719

8.5.1 Metaprogramming in Financial Modeling

In the context of financial modeling, macros can be used to simplify repetitive or complex code patterns, enforce certain conventions or constraints, or generate code based on data or configuration.

Here are a few potential use cases of macros in financial modeling. Again, these are more advanced use-cases but knowing that these paths exist may benefit your work in the future.

  1. Defining custom DSLs (Domain-Specific Languages): Macros can be used to create expressive and concise DSLs tailored to financial modeling. For example, a macro could allow defining financial contracts using a syntax closer to the domain language, which then gets expanded into the underlying implementation code.

  2. Automating boilerplate code: Macros can help reduce code duplication by generating common patterns or boilerplate code. This can include generating accessor functions3, constructors, or serialization logic based on type definitions.

  3. Enforcing conventions and constraints: Macros can be used to enforce coding conventions, such as naming rules or type checks, by automatically transforming code that doesn’t adhere to the conventions. They can also be used to add runtime assertions or checks based on certain conditions.

  4. Optimizing performance: Macros can be used to perform code optimizations at compile-time. For example, a macro could unroll loops, inline functions, or specialize generic code based on specific types or parameters, resulting in more efficient runtime code.

  5. Generating code from data: Macros can be used to generate code based on external data or configuration files. For example, a macro could read a specification file and generate the corresponding financial contract types and functions.

  1. And projections, which is handled by defining a ProjectionKind , such as a cashflow or accounting basis. This topic is covered in more detail in the FinanceModels.jl documentation.↩︎

  2. @time is a simple, built-in function. For true benchmarking purposes, see Section 24.4.↩︎

  3. Accessor functions are useful when working with nested data structures. For example, if you have a struct within a struct and want to conveniently access an inner structs field.↩︎